Rabu, 12 Juni 2013
Eksponen
Bit ke 23 sampai ke 30 berisi eksponen. Eksponen adalah sebuah integer, tapi bisa negatif, nol atau positif. Kamu mungkin menduga bahwa kita akan menggunakan 8bit integer two komplemen, namun kenyataannya kita menggunakan cara lain.
Eksponen tersusun menggunakan skema integer biased. Integer biased ini secara rekayasa merupakan pembiasan dari integer biasa yang seolah-olah ditambah dengan angka +127 jadi jika angka 0 melalui perhitungan biasa sedang direpresentasikan oleh 8bit maka sebenarnya angka tersebut sedang merepresentasikan angka 127. Angka 128 direpresentasikan dengan eksponen 1; angka 126 direpresentasikan dengan eksponen -1.
kita tentunya sudah membaca tadi bahwa mantissa selalu seolah-olah sudah memiliki "1," di depannya. lalu bagaimana jika kita sedang merepresentasikan pecahan "0,0" ?
Bagaimana Mantissa Berfungsi
Secara angka nol di depan sebuah koma bukanlah angka penting, maka kita selalu mendapati sebuah angka yang diawali dengan 1,
misal kita ingin merepresentasikan sebuah pecahan biner floating point 00011,00101101
angka 0 di depan koma hilangkan menjadi 11,00101101
kemudian majukan koma nya sehingga tepat diantara angka pertama dan kedua sehingga menjadi 1,100101101 x 2^1
karena setiap mantissa selalu direkayasa memiliki angka 1, di depannya sehingga angka tersebut tidak akan masuk ke mantissa, jadi yang ada di mantissa hanyalah angka yang ada di belakang angka 1,
yaitu 1,100101101 menjadi 100101101, ini lah yang akan mengisi mantissa sementara eksponen akan diisi dengan angka 2^1
jadi isi mantissanya adalah 10010110100000000000000
Quest 13: Apakah mantissa selalu 0 atau positif?
Jawab: ya tanda negatif bukanlah bagian dari mantissa
misal kita ingin merepresentasikan sebuah pecahan biner floating point 00011,00101101
angka 0 di depan koma hilangkan menjadi 11,00101101
kemudian majukan koma nya sehingga tepat diantara angka pertama dan kedua sehingga menjadi 1,100101101 x 2^1
karena setiap mantissa selalu direkayasa memiliki angka 1, di depannya sehingga angka tersebut tidak akan masuk ke mantissa, jadi yang ada di mantissa hanyalah angka yang ada di belakang angka 1,
yaitu 1,100101101 menjadi 100101101, ini lah yang akan mengisi mantissa sementara eksponen akan diisi dengan angka 2^1
jadi isi mantissanya adalah 10010110100000000000000
Quest 13: Apakah mantissa selalu 0 atau positif?
Jawab: ya tanda negatif bukanlah bagian dari mantissa
Lebih jauh pada Mantissa
Mantissa merepresentasikan angka dalam basis dua sepanjang 24bit. notasi posisinya seperti berikut ini:
1.xxxxxxxxxxxxxxxxxxxxxxx
di dalam tabel sebelumnya kita sudah melihat bahwa mantissa hanya terdiri dari 23bit yang artinya 1bit tambahan hanyalah rekayasa. Misal untuk angka 1.11110000101101101010001 maka mantissa hanya akan berisi dengan angka 11110000101101101010001.
1.xxxxxxxxxxxxxxxxxxxxxxx
di dalam tabel sebelumnya kita sudah melihat bahwa mantissa hanya terdiri dari 23bit yang artinya 1bit tambahan hanyalah rekayasa. Misal untuk angka 1.11110000101101101010001 maka mantissa hanya akan berisi dengan angka 11110000101101101010001.
IEEE 754 Floating Point
Sebuah single presisi floating point merujuk pada IEEE 754 adalah sejumlah 32bit panjang. Bit-bit ini dibagi-bagi menjadi sejumlah tetap sebagai berikut:
Bit 0 sampai 22 digunakan untuk mantissa; bit 23 sampai 30 digunakan untuk eksponen; dan bit 31 adalah sign bit. Kolom mantissa dan kolom eksponen bekerja seperti bagian yang sama pada notasi ilmiah. Sign bit menjadi tanda untuk keseluruhan notasi apakah angka tersebut 0 yang artinya positif ataukah 1 yang artinya negatif.
Quest 11: kamu telah melihat instruksi bltz yang artinya branch jika sebuah integer 32bit adalah di bawah nol atau angka tersebut negatif. Hal ini bekerja dengan cara dia mengecek bit ke terakhir apakah dia 1 atau 0.
apakah cara yang sama juga berlaku untuk single presisi?
Jawab: Ya
Bit 0 sampai 22 digunakan untuk mantissa; bit 23 sampai 30 digunakan untuk eksponen; dan bit 31 adalah sign bit. Kolom mantissa dan kolom eksponen bekerja seperti bagian yang sama pada notasi ilmiah. Sign bit menjadi tanda untuk keseluruhan notasi apakah angka tersebut 0 yang artinya positif ataukah 1 yang artinya negatif.
Quest 11: kamu telah melihat instruksi bltz yang artinya branch jika sebuah integer 32bit adalah di bawah nol atau angka tersebut negatif. Hal ini bekerja dengan cara dia mengecek bit ke terakhir apakah dia 1 atau 0.
apakah cara yang sama juga berlaku untuk single presisi?
Jawab: Ya
Senin, 10 Juni 2013
Digit Angka yang Tetap
Tiap-tiap notasi diwakili oleh 8 digit. dua digit digunakan untuk "float" koma desimal. Sisanya enam digit digunakan untuk mewakili angka.
Angka di dalam digit mantissa disebut presisi dari angka floating point. Saat kita mulai membicarakan floating point, presisinya adalah sejumlah bit yang ada di mantissa. Dengan sebuah 32bit single presisi floating point mantissa adalah 24bit. jadi single presisi floating point mempunyai 24bit presisi.
Perhatian: kadang-kadang dalam bahasa yang salah orang-orang menyebutkan bahwa nilai single presisi mempunyai 32bit presisi, tapi ini tidak benar.
Perhatian yang lain: mantissa menggunakan 23bit untuk merepresentasikan presisi 24bit. Trik ini akan dijelaskan selanjutnya.
Quest 10: berapa banyak mantissa yang bisa direpresentasikan oleh single presisi?
Jawab: sebuah mantissa mempunyai 23bit jadi ada sebanyak 2^23 pola yang tersedia.
Angka di dalam digit mantissa disebut presisi dari angka floating point. Saat kita mulai membicarakan floating point, presisinya adalah sejumlah bit yang ada di mantissa. Dengan sebuah 32bit single presisi floating point mantissa adalah 24bit. jadi single presisi floating point mempunyai 24bit presisi.
Perhatian: kadang-kadang dalam bahasa yang salah orang-orang menyebutkan bahwa nilai single presisi mempunyai 32bit presisi, tapi ini tidak benar.
Perhatian yang lain: mantissa menggunakan 23bit untuk merepresentasikan presisi 24bit. Trik ini akan dijelaskan selanjutnya.
Quest 10: berapa banyak mantissa yang bisa direpresentasikan oleh single presisi?
Jawab: sebuah mantissa mempunyai 23bit jadi ada sebanyak 2^23 pola yang tersedia.
e
Membuat pangkat dengan cara menulis angka yang kecil di atas angka lainnya tidak cocok dengan program. Sebuah notasi sedikit diubah agar bisa digunakan di komputer baik sebagai input maupun output text.
1,38502 × 10^+03 = 1,38502e+03
1,38502 × 10^-03 = 1,38502e-03
-1,38502 × 10^+03 = -1,38502e+03
-1,38502 × 10^-03 = -1,38502e-03
Perhatian: untuk SPIM hanya huruf "e" kecil yang berlaku untuk notasi ini. (beberapa software sistem seperti JAVA memperbolehkan menggunakan huruf besar atau hirif kecil).
Quest 9: Berapa banyak digit kah yang diperlukan untuk notasi di atas? Berapa digit untuk mantissa dan berapa digit untuk eksponen?
Jawab: 8. 6 digit mantisa, 2 digit eksponen
1,38502 × 10^+03 = 1,38502e+03
1,38502 × 10^-03 = 1,38502e-03
-1,38502 × 10^+03 = -1,38502e+03
-1,38502 × 10^-03 = -1,38502e-03
Perhatian: untuk SPIM hanya huruf "e" kecil yang berlaku untuk notasi ini. (beberapa software sistem seperti JAVA memperbolehkan menggunakan huruf besar atau hirif kecil).
Quest 9: Berapa banyak digit kah yang diperlukan untuk notasi di atas? Berapa digit untuk mantissa dan berapa digit untuk eksponen?
Jawab: 8. 6 digit mantisa, 2 digit eksponen
Nilai Negatif
Notasi untuk angka negatif memiliki tanda negatif di depan digit pertama
-1,38502 × 10^03 = -(1,38502 × 10^03) = -1385,02
Notasi untuk angka yang lebih kecil mempunyai dua tanda negatif, satu untuk menegatifkan angka, satu lagi untuk menggerakkan koma pecahan ke kiri.
-1,38502 × 10^-3 = -(1,38502 × 10^-3) = -0,00138502
-1,38502 × 10^03 = -(1,38502 × 10^03) = -1385,02
Notasi untuk angka yang lebih kecil mempunyai dua tanda negatif, satu untuk menegatifkan angka, satu lagi untuk menggerakkan koma pecahan ke kiri.
-1,38502 × 10^-3 = -(1,38502 × 10^-3) = -0,00138502
Eksponen Negatif
Eksponen menunjukkan kelipatan 10 dari mantissa, sejauh mana float menunjukkan koma desimal.
10^+n artinya gerakkan tanda koma ke kanan
10^-n artinya gerakkan tanda koma ke kiri
1,82371 × 10^1 = 1,82371 × 10 = 18.2371 (koma bergerak 1 langkah ke kanan)
1,82371 × 10^-1 = 1,82371 × ,1 = ,182371 (koma bergerak 1 langkah ke kiri)
1,82371 × 10^2 = 1,82371 × 100 = 182.371 (koma bergerak 2 langkah ke kanan)
1,82371 × 10^-2 = 1,82371 × ,01 = ,0182371 (koma bergerak 2 langkah ke kiri)
Quest 7: tulislah 0,000456 dalam notasi ilmiah
Jawab: 0,000456 = 4,56 × 10^-4
10^+n artinya gerakkan tanda koma ke kanan
10^-n artinya gerakkan tanda koma ke kiri
1,82371 × 10^1 = 1,82371 × 10 = 18.2371 (koma bergerak 1 langkah ke kanan)
1,82371 × 10^-1 = 1,82371 × ,1 = ,182371 (koma bergerak 1 langkah ke kiri)
1,82371 × 10^2 = 1,82371 × 100 = 182.371 (koma bergerak 2 langkah ke kanan)
1,82371 × 10^-2 = 1,82371 × ,01 = ,0182371 (koma bergerak 2 langkah ke kiri)
Quest 7: tulislah 0,000456 dalam notasi ilmiah
Jawab: 0,000456 = 4,56 × 10^-4
Notasi Ilmiah
Untuk mengetasi masalah ini IEEE ( institut Elektrikal dan Elektronik Engineer) membuat sebuah standar untuk floating point. Inilah yang disebut IEEE 754 standar, rilis pada tahun 1985 setelah bertahun-tahun dikembangkan. Semua hardware dan software akhirnya mengikuti standar ini (banyak processor juga support dengan standar lain bagaimanapun juga).
Ide dari floating point muncul dari notasi ilmiah untuk angka. Kamu mungkin pernah melihat ini sebelumnya. Berikut adalah notasi ilmiah untuk angka:
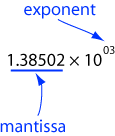
Mantisa selalu mempunyai koma desimal di antara angka pertama dan kedua. Rumus di atas mempunyai arti:
1,38502 × 1000 = 1385,02
Koma desimal bergerak "float" ke mana dia diartikan. Pengaruhnya adalah mantisa memberikan digitnya sedangkan eksponen mengatakan dimana tanda koma nya seharusnya berada.
Quest 6: tulislah notasi ilmiah dari 243,92
Jawab: 243,92 = 2,4392 × 10^2
Ide dari floating point muncul dari notasi ilmiah untuk angka. Kamu mungkin pernah melihat ini sebelumnya. Berikut adalah notasi ilmiah untuk angka:

Mantisa selalu mempunyai koma desimal di antara angka pertama dan kedua. Rumus di atas mempunyai arti:
1,38502 × 1000 = 1385,02
Koma desimal bergerak "float" ke mana dia diartikan. Pengaruhnya adalah mantisa memberikan digitnya sedangkan eksponen mengatakan dimana tanda koma nya seharusnya berada.
Quest 6: tulislah notasi ilmiah dari 243,92
Jawab: 243,92 = 2,4392 × 10^2
Kompabilitas Floating Point
Sampai pada tahun 1985 tiap manufaktur hardware mempunyai jenis floating pointnya sendiri-sendiri. Jeleknya, mesin yang berbeda dari manufaktur yang sama mungkin memiliki floating point yang berbeda! Dan ketika floating tidak support di hardaware, kompiler yang berbeda akan menghasilkan floating point dengan jenis yang berbeda.
Situasi menjadi sangat mengerikan. Mempertimbangkan sebuah tape yang berisi data yang ditulis oleh mainframe IBM. Sekarang tape tersebut harus dibaca oleh minikomputer DEC. Katakanlah bit-bit di dalam tape tersebut bisa dibaca dengan benar. Tapi DEC menggunakan jenis floating point yang berbeda dari IBM. Menerjemahkan bit-bit tersebut sangatlah susah! Masalah seperti ini yang umumnya disebut "legacy data". NASA memiliki banyak sekali tape dari berbagai misi luar angkasa yang ditulis dalam bermacam-macam format. Sebagian data ini sudah tidak terurus karena kurangnya program yang bisa membacanya.
Quest 5: haruskan sebuah perhitungan angka dijalankan pada dua komputer menghasilkan hasil yang sama?
Jawab: Ya. tapi sebelum digunakannya standar floating point, hal ini tidak menjadi sesuatu yang benar
Situasi menjadi sangat mengerikan. Mempertimbangkan sebuah tape yang berisi data yang ditulis oleh mainframe IBM. Sekarang tape tersebut harus dibaca oleh minikomputer DEC. Katakanlah bit-bit di dalam tape tersebut bisa dibaca dengan benar. Tapi DEC menggunakan jenis floating point yang berbeda dari IBM. Menerjemahkan bit-bit tersebut sangatlah susah! Masalah seperti ini yang umumnya disebut "legacy data". NASA memiliki banyak sekali tape dari berbagai misi luar angkasa yang ditulis dalam bermacam-macam format. Sebagian data ini sudah tidak terurus karena kurangnya program yang bisa membacanya.
Quest 5: haruskan sebuah perhitungan angka dijalankan pada dua komputer menghasilkan hasil yang sama?
Jawab: Ya. tapi sebelum digunakannya standar floating point, hal ini tidak menjadi sesuatu yang benar
Floating Point Zaman dulu
Komputer digital pertama (menurut beberapa sumber) yakni Z3, dibuat oleh Konrad Zuse pada tahun 1941 menggunakan representasi floating point. Komputer ini memiliki clock lima sampai sepuluh Hertz dan sebuah memory 64 word 22bit! (mesin pendahulunya Z1 juga menggunakan floating point tapi masih belum bisa disebut sebagai komputer karena susah diprogram).
Komputer zama dulu dibuat untuk melakukan perhitungan sain maupun teknik jadi tidak mengherankan jika penemuan floating poin terjadi pada saat yang sama. Di tahun-tahun berikutnya disadari bahwa komputer menjadi alat yang sangat berguna, dan bukan hanya menjadi kalkulator. Seringkali floating point tidak didukung.
Banyak sekali minikomputer dan microprocessor dulu tidak support floating point pada hardware. Sebagai contoh, chip processor intel sebelum 80486 tidak mendukung floating point secara langsung. Sebuah operasi floating point di dalam program (ditulis dalam C, misalnya) dikompile ke dalam barisan intruksi manipulasi bit yang membutuhkan operasi-operasi. Komputer graphic maupun teknik seringkali memiliki chip tambahan yang mengoperasikan floating point secara hardware.
Processor MIPS sangatlah kuat untuk floating point, dan telah mendukung standar IEEE dari sejak awal. Chip MIPS seringkali digunakan pada teknik tinggi dan workstation grafis dan sangat terkenal dengan floating pointnya yang cepat.
Jumat, 07 Juni 2013
Floating Point
Ide pokok dari floating point adalah kita memiliki sejumlah bit yang tetap (misalkan 32 atau 64) dan tanda koma sebagai identitas pecahan berada di mana saja diantara bit-bit tersebut sesuai kebutuhan. Tentu saja, komputer hanya menyimpan pola-pola bit, lalu bagaimana kamu bisa mengetahui berada di mana tanda koma nya? beberapa pola bit di dalam floating point menerjemahkan atau mengartikan dimana letak tanda koma tersebut.
Skema representasi floating point bisa merepresentasikan angka yang sangat kecil atau yang sangat besar. Ketika kita sedang mengoperasikan floating point, maka biner dengan posisi koma yang benar atau sejajar. Programmer tidak bekerja untuk menjaga tanda-tanda ini bekerja dengan benar, programmer hanya memasukkan nilainya kemudian menyerahkan segalanya ke mesin.
Quest 3: apakah floating point adalah ide modern atau ide kuno?
Jawab: ide kuno
Skema representasi floating point bisa merepresentasikan angka yang sangat kecil atau yang sangat besar. Ketika kita sedang mengoperasikan floating point, maka biner dengan posisi koma yang benar atau sejajar. Programmer tidak bekerja untuk menjaga tanda-tanda ini bekerja dengan benar, programmer hanya memasukkan nilainya kemudian menyerahkan segalanya ke mesin.
Quest 3: apakah floating point adalah ide modern atau ide kuno?
Jawab: ide kuno
Kenapa Floating Point?
Representasi floating point membuat perhitungan numerik menjadi lebih mudah. Kamu boleh saja membuat sebuah program yang hanya berisi integer atau fixed point, namun akan menjadi sulit atau rawan error. Misalnya kamu membuat program, yang mana integer di dalam program tersebut adalah representasi 100kali dari data. Integer 2345 misalnya jika di dalam data maka akan menjadi 23.45. Selama kamu konsisten semua akan berjalan dengan baik.
Hal yang sama juga berlaku di fixed point, kamu akan secara konsisten mengatakan sebuah integer yang secara ilusi mempunyai koma pecahan desimal di tengah-tengah data tersebut. Meskipun pada kenyataannya tidak ada tanda koma di situ namun secara konvensi atau secara konsisten kamu menganggapnya ada.
Namun tidaklah mudah untuk mengatakan kamu bisa konsisten. Seorang programmer harus tau di mana letak koma yang menjadi tanda pecahan desimal, apakah di tengah-tengah sebuah data atau di mana. Kadang kala ada sebuah program yang membuatmu untuk menggunakan tanda pecahan yang bisa berubah-ubah posisinya, misalnya sebuah program peta, kamu akan menjumpai angka (katakanlah 0,00000010 meter sampai 0,00001000 meter) kasus-kasus semacam ini dimana kamu memerlukan bilangan yang nilai pecahannya bisa merepresentasikan pecahan desimal lebih presisi atau lebih luwes dengan cara menggerakkan tanda koma yang ada di pecahan tersebut.
Quest 2: Ketika sebuah tanda pecahan desimal bergerak baik ke kanan atau ke kiri untuk memberikan pernyataan angka pecahan yang lebih luwes, disebut apakah tanda koma itu?
Jawab: Float
Hal yang sama juga berlaku di fixed point, kamu akan secara konsisten mengatakan sebuah integer yang secara ilusi mempunyai koma pecahan desimal di tengah-tengah data tersebut. Meskipun pada kenyataannya tidak ada tanda koma di situ namun secara konvensi atau secara konsisten kamu menganggapnya ada.
Namun tidaklah mudah untuk mengatakan kamu bisa konsisten. Seorang programmer harus tau di mana letak koma yang menjadi tanda pecahan desimal, apakah di tengah-tengah sebuah data atau di mana. Kadang kala ada sebuah program yang membuatmu untuk menggunakan tanda pecahan yang bisa berubah-ubah posisinya, misalnya sebuah program peta, kamu akan menjumpai angka (katakanlah 0,00000010 meter sampai 0,00001000 meter) kasus-kasus semacam ini dimana kamu memerlukan bilangan yang nilai pecahannya bisa merepresentasikan pecahan desimal lebih presisi atau lebih luwes dengan cara menggerakkan tanda koma yang ada di pecahan tersebut.
Quest 2: Ketika sebuah tanda pecahan desimal bergerak baik ke kanan atau ke kiri untuk memberikan pernyataan angka pecahan yang lebih luwes, disebut apakah tanda koma itu?
Jawab: Float
Selasa, 07 Mei 2013
BAB 30 — IEEE 754 Floating Point
Bab ini adalah tentang standar IEEE 754 floating point. Ini adalah standar untuk angka floating point yang digunakan oleh komputer-komputer saat ini dan bahasa pemrograman sejak 1985. Java floating point (ada di virtual processornya) dan MIPS floating point (ada di hardwarenya) sesuai dengan standard ini.
Topik:
Topik:
- Kenapa menggunakan floating point?
- Sejarah floating point
- Notasi ilmiah
- Presisi dari floating point
- Standar IEEE 754 floating point
- Konversi ke notasi floating point
Quest 1: Apakah benar-benar penting bahwa processor harus support dengan data jenis floating point?
Jawab: Tidak. Semua yang dibutuhkan processor hanyalah instruksi-intruksi dasar. Segala sesuatu bisa dibuat dari itu termasuk floating point.
Senin, 06 Mei 2013
Menghitung tiap-tiap float
Gunakan jenis loop for untuk mendapatkan hitungan yang aman. Hitunglah nilai-nilai floating dari variable 0 sampai 100.
double x;
int j;
for ( j = 0; j < 100; j++ )
{
x = j/10.0;
// do something with x
}
Hampir semua, menghitung floating point dengan jenis double precision bisa berhasil. Dan yang lebih presisi lagi adalah:
double x;
int j;
for ( j = 0; j < 160; j++ )
{
x = j/16.0;
// do something with x
}
Hal ini lebih baik karena 1/16 bisa direpresentasikan oleh biner dengan tepat.
Quest 19: apakah representasi floating point sama dengan fixed poin yang sedang kita bahas saat ini?
Jawab: No. Mereka berhubungan namun floating point lebih canggih. Bab selanjutnya kita akan membahas floating point
double x;
int j;
for ( j = 0; j < 100; j++ )
{
x = j/10.0;
// do something with x
}
Hampir semua, menghitung floating point dengan jenis double precision bisa berhasil. Dan yang lebih presisi lagi adalah:
double x;
int j;
for ( j = 0; j < 160; j++ )
{
x = j/16.0;
// do something with x
}
Hal ini lebih baik karena 1/16 bisa direpresentasikan oleh biner dengan tepat.
Quest 19: apakah representasi floating point sama dengan fixed poin yang sedang kita bahas saat ini?
Jawab: No. Mereka berhubungan namun floating point lebih canggih. Bab selanjutnya kita akan membahas floating point
Berhitung dengan Integer
Jika tujuan fragmen program adalah berhitung sampai 100kali maka, berhitung di dalam loop bisa menggunakan bilangan bulat, berikut adalah contoh perbaikannya:
int x;
for ( x = 0; x < 100; x++ )
{
System.out.println("Crimson and Clover");
}
(sudah umum untuk menulis program dengan konvensi seperti ini meskipun program bisa mecapai x=100 dengan tepat.) berikut adalah solusi yang buruk:
float x;
for ( x = 0.0; x < 10.0; x += 0.1 )
{
System.out.println("Crimson and Clover");
}
Solusi tersebut mugkin memang bekerja seperti yang diharapkan. namun terdapat risiko kalau loop berhitung sampai 101 kali
int x;
for ( x = 0; x < 100; x++ )
{
System.out.println("Crimson and Clover");
}
(sudah umum untuk menulis program dengan konvensi seperti ini meskipun program bisa mecapai x=100 dengan tepat.) berikut adalah solusi yang buruk:
float x;
for ( x = 0.0; x < 10.0; x += 0.1 )
{
System.out.println("Crimson and Clover");
}
Solusi tersebut mugkin memang bekerja seperti yang diharapkan. namun terdapat risiko kalau loop berhitung sampai 101 kali
Infinity Loop yang Tersembunyi
Jika kita menggunakan basis 10, maka 0,1 akan ditambahkan ke x sebanyak 100kali sampai mencapai 10,0 dengan tepat. Tapi komputer menggunakan basis dua floating point, yang artinya tidak merepresentasikan nilai 0,1 secara tepat. Variabel x bisa jadi tidak akan mencapai nilai 10,0 dengan tepat dan program tidak akan looping tanpa henti.
float x;
for ( x = 0.0; x != 10.0; x += 0.1 )
{
System.out.println("Crimson and Clover");
}
Tidak hanya fixed point yang tidak bisa merepresentasikan sepersepuluh dengan benar, tetapi juga floating point yang biasa dipakai di bahasa pemrograman juga memiliki masalah yang sama.
float x;
for ( x = 0.0; x != 10.0; x += 0.1 )
{
System.out.println("Crimson and Clover");
}
Tidak hanya fixed point yang tidak bisa merepresentasikan sepersepuluh dengan benar, tetapi juga floating point yang biasa dipakai di bahasa pemrograman juga memiliki masalah yang sama.
Code yang Berbahaya
Berikut adalah sebuah fragmen program di Java. (Bisa juga di C atau C++). Apakah ada sesuatu di dalam program tersebut yang perlu kamu khawatirkan?
float x;
for ( x = 0.0; x != 10.0; x += 0.1 )
{
System.out.println("Crimson and Clover");
}
Quest 16: Berapa kali kah Crimson and Clover akan dicetak?
Jawab: Terus menerus
float x;
for ( x = 0.0; x != 10.0; x += 0.1 )
{
System.out.println("Crimson and Clover");
}
Quest 16: Berapa kali kah Crimson and Clover akan dicetak?
Jawab: Terus menerus
Hasil yang tidak berhenti
Pada gambar di bawah kita menggunakan algoritma untuk mengkonversi 0,110 menjadi biner.
Algoritma ini tidak pernah berhenti dan menghasilkan pola yang sama 0,2 0,4 0,8 1,6 0,6 1,2 0,2 tanpa henti. Hasilnya pola biner 0011 juga tidak akan berhenti seterusnya.
Quest: 15: Bisakah satu per tiga direpresentasikan secara presisi oleh desimal?
Jawab: Tidak 1/3 akan menghasilkan 0,3333.... secara tak terhingga
Masalah dengan sepersepuluh bukanlah masalah spesial yang perlu dihindari, karena dengan semua basis yang ada pasti mempunyai pecahan yang tidak presisi.
Algoritma ini tidak pernah berhenti dan menghasilkan pola yang sama 0,2 0,4 0,8 1,6 0,6 1,2 0,2 tanpa henti. Hasilnya pola biner 0011 juga tidak akan berhenti seterusnya.
Fakta yang tidak terduga: nilai "sepersepuluh" tidak bisa direpresentasikan secara presisi oleh pecahan biner.Hal ini benar di dalam biner notasi posisi maupun floating point yang digunakan di bahasa pemrograman. Kadang kadang hal ini membutuhkan pertimbangan penting ketika akurasi tinggi diperlukan.
| Decimal | Binary so far | |
|---|---|---|
| Start | 0,1 | 0, |
| ×2 | 0,2 | 0,0 |
| ×2 | 0,4 | 0,00 |
| ×2 | 0,8 | 0,000 |
| ×2 | 1,6 | 0,0001 |
| ,6 | 0,0001 | |
| ×2 | 1,2 | 0,00011 |
| 0,2 | 0,00011 | |
| ×2 | 0,4 | 0,000110 |
| ×2 | 0,8 | 0,0001100 |
| ×2 | 1,6 | 0,00011001 |
| ,6 | 0,00011001 | |
| ×2 | 1,2 | 0,000110011 |
| 0,2 | 0,000110011 | |
| ×2 | 0,4 | 0,0001100110 |
| ×2 | 0,8 | 0,00011001100 |
| Result | 0,00011001100... |
Quest: 15: Bisakah satu per tiga direpresentasikan secara presisi oleh desimal?
Jawab: Tidak 1/3 akan menghasilkan 0,3333.... secara tak terhingga
Masalah dengan sepersepuluh bukanlah masalah spesial yang perlu dihindari, karena dengan semua basis yang ada pasti mempunyai pecahan yang tidak presisi.
Konversi Representasi dari Desimal ke Biner
Seringkali kamu membutuhkan mengkonversi angka desimal semisal 7,625 menjadi sebuah angka biner. Pertama-tama konversi angka bulat nya (dalam kasus ini 7) menjadi biner (111 dalam kasus ini). Tambahkan koma sebagai pemisah pecahan kemudian konversi angka pecahan tersebut menjadi biner.
Sebagai contoh 7,625 adalah 111,1012 di kasus ini konversi berhenti setelah pecahan mencapai angka nol. Hal seperti ini tidak selamanya berhasil.
Untuk mengkonversi pecahan desimal menjadi pecahan biner: Kalikan angka tersebut dengan dua, kemudian ambil angka yang berada di depan koma, lakukan ini sampai isi dari pecahan tersebut menjadi nol.
| Decimal | Binary so far | |
|---|---|---|
| Start | 0,625 | 0, |
| ×2 | 1,250 | 0,1 |
| ,250 | 0,1 | |
| ×2 | 0,500 | 0,10 |
| ,500 | 0,10 | |
| ×2 | 1,000 | 0,101 |
| Result | ,000 | 0,101 |
Geser ke kiri satu bit
Mari kita kembali ke corat-coret kertas dan pensil. Berikut adalah angka biner:
Dan dari pola di atas kita geser ke kiri sejauh 1 langkah
Quest 12: Apa yang dihasilkan dari geser ke kiri sejauh 1 langkah?
Jawab: Dikalikan dengan dua
0001.0100 = 1.2510
Dan dari pola di atas kita geser ke kiri sejauh 1 langkah
0010.1000 = 2.5010
Quest 12: Apa yang dihasilkan dari geser ke kiri sejauh 1 langkah?
Jawab: Dikalikan dengan dua
Minggu, 05 Mei 2013
Infinity angka yang hilang
Presisi yang terbatas dari fixed point (ataupun floating point) merupakan sebuah masalah bagi programmer. Bahkan menggunakan 64bit double precision floating point (misal type data java double) presisi masih terbatasi. Hanya 264 angka yang bisa di representasikan. Ini memang banyak tapi tetap saja ada sejumlah infinity real number yang tidak bisa direpresentasikan.
(Jika kamu belum paham kalkulus tidak usah khawatir, hanya berpikirlah bahwa kamu bisa membuat pecahan yang tidak terbatas)
Quest 11: Berapa banyak digit yang dimiliki oleh nilai phi?
Jawab: infinity
(Jika kamu belum paham kalkulus tidak usah khawatir, hanya berpikirlah bahwa kamu bisa membuat pecahan yang tidak terbatas)
Quest 11: Berapa banyak digit yang dimiliki oleh nilai phi?
Jawab: infinity
Presisi yang terbatas
Ini pertanyaan mudah. Jika N bit digunakan maka akan ada sejumlah 2N banyaknya yang bisa direpresentasikan oleh digit tersebut, tidak peduli apa jenis yang direpresentasikannya itu. 8bit bisa merepresentasikan sejumlah 256 integer unsigned, 256 integer two complement, maupun 256 angka pecahan (fixed point) dan seterusnya. Berikut adalah gambar garis yang menunjukkan 256 nilai yang bisa direpresentasikan oleh fixed point.
Nilai terkecil adalah zero 00000000 nilai terbesar adalah 15,9375. Angka terkecil setelah nol adalah 0,0625 Semua nilai yang direpresentasikan oleh bilangan ini adalah merupakan kelipatan dari 0,0625.
Cara lain untuk memahami fixed point notation adalah dengan menganggap bahwa 8bit akan menghasilkan 0-255 angka yang angka terkecilnya merupakan 0,0625. dan setiap naik satu angka merupakan kelipatan dari nilai dasarnya yaitu 0,0625. Misal jika
00000001 tanpa koma = 1
00000010 tanpa koma = 1+1 = 2
0000,0001 dengan koma = 0,0625
0000,0010 dengan koma = 0,0625+0,0625 = 0,125
Jarak antara dua buah bilangan bulat jika menggunkan metode ini hanya 16 pembagian, secara 1/16 = 0,0625. hal ini membuat metode bilangan menjadi tidak efektif karena akan menimbulkan banyak gaps diantara tiap angka.
Masalah penting: dalam sebuah pecahan dituntut sebuah presisi yang dinamis, dan tingkat ketelitian yang sesuai agar bisa layak dipakai sebagai sebuah representasi pecahan.
Quest 10: (ingat kalkulus) berapakah jumlah real number yang berada di antara 0,0 sampai 0,0625?
Jawab: Tak terhingga
Nilai terkecil adalah zero 00000000 nilai terbesar adalah 15,9375. Angka terkecil setelah nol adalah 0,0625 Semua nilai yang direpresentasikan oleh bilangan ini adalah merupakan kelipatan dari 0,0625.
Cara lain untuk memahami fixed point notation adalah dengan menganggap bahwa 8bit akan menghasilkan 0-255 angka yang angka terkecilnya merupakan 0,0625. dan setiap naik satu angka merupakan kelipatan dari nilai dasarnya yaitu 0,0625. Misal jika
00000001 tanpa koma = 1
00000010 tanpa koma = 1+1 = 2
0000,0001 dengan koma = 0,0625
0000,0010 dengan koma = 0,0625+0,0625 = 0,125
Jarak antara dua buah bilangan bulat jika menggunkan metode ini hanya 16 pembagian, secara 1/16 = 0,0625. hal ini membuat metode bilangan menjadi tidak efektif karena akan menimbulkan banyak gaps diantara tiap angka.
Masalah penting: dalam sebuah pecahan dituntut sebuah presisi yang dinamis, dan tingkat ketelitian yang sesuai agar bisa layak dipakai sebagai sebuah representasi pecahan.
Quest 10: (ingat kalkulus) berapakah jumlah real number yang berada di antara 0,0 sampai 0,0625?
Jawab: Tak terhingga
Algoritma penambahan biner sudah benar
Algoritma penambahan biner, berhasil digunakan sebagai penjumlahan untuk pecahan fixed point. Dulu komputer jadul dan kalkulator menggunakan rangkaian elektronik yang sama untuk digunakan sebagai penjumlahan integer biner (baik two complemen maupun unsigned) dan penjumlahan biner pecahan fixed point. Hal ini sepertinya menjanjikan.
Bagaimanapun fixed point tidak sebagus daripada floating point yang sekarang sudah menggantikannya. Floating point akan dibahas di bab selanjutnya.
Quest 9: berapa banyak nilai yang bisa direpresentasikan menggunakan 8bit fixed point notation?
Jawab: 28 = 256
Bagaimanapun fixed point tidak sebagus daripada floating point yang sekarang sudah menggantikannya. Floating point akan dibahas di bab selanjutnya.
Quest 9: berapa banyak nilai yang bisa direpresentasikan menggunakan 8bit fixed point notation?
Jawab: 28 = 256
Cara menjumlahkan fixed point
Berikut adalah angka yang lain 00010100. Angka ini merepresentasikan desimal 1,25 . dan berikut adalah algoritma umum yang biasa digunakan untuk menjumlahkan dua buah pecahan biner
Quest 8: Tentu saja yang jadi pertanyaan adalah apakah penjumlahan pecahan biner menghasilkan hasil yang benar seperti pada penjumlahan pecahan desimal?
| fixed point | as decimal | |
| 01101001 | 6,5625 | |
| 00010100 | 1,2500 | |
| 01111101 | 7,8125 |
Quest 8: Tentu saja yang jadi pertanyaan adalah apakah penjumlahan pecahan biner menghasilkan hasil yang benar seperti pada penjumlahan pecahan desimal?
Notasi Fixed Point
Dengan kertas dan pensil, kamu bebas menulis berapa digit yang kamu mau. Tapi komputer (biasanya) menggunakan digit yang dibatasi sebagai perwakilan dari jenis data tertentu. Sebagai contoh interger 32bit, jadi bisakah jumlah bit yang terbatas ini digunakan untuk mewakili pecahan?
Ya. Mari kita lihat sejenak metode kuno yang sekarang sudah jarang lagi digunakan. Pada zaman dahulu, kalkulator elektronik dan komputer menggunakan notasi titik tetap untuk mengekspresikan pecahan. Dengan notasi titik tetap, angka diekspresikan dengan cara menganggap sejumlah digit tertentu (misal delapan) dan koma/titik yang memisahkan antara bilangan bulat dan pecahan ini di anggap pasti berada di sela-sela digit tersebut.
Sebagai contoh, mari kita anggap sebuah angka biner yang menggunakan notasi titik tetap, sebuah koma berada di tengah-tengah 8bit angka ini. Sekarang coba kamu terjemahkan angka tersebut menjadi sebuah bilangan desimal:
Quest 7:
Di skema berikut ini pola bit 01101001 merepresentasikan angka berapa?
Jawab: 4 + 2 + 0,5 + 0,0625 = 6,5625
Ya. Mari kita lihat sejenak metode kuno yang sekarang sudah jarang lagi digunakan. Pada zaman dahulu, kalkulator elektronik dan komputer menggunakan notasi titik tetap untuk mengekspresikan pecahan. Dengan notasi titik tetap, angka diekspresikan dengan cara menganggap sejumlah digit tertentu (misal delapan) dan koma/titik yang memisahkan antara bilangan bulat dan pecahan ini di anggap pasti berada di sela-sela digit tersebut.
Sebagai contoh, mari kita anggap sebuah angka biner yang menggunakan notasi titik tetap, sebuah koma berada di tengah-tengah 8bit angka ini. Sekarang coba kamu terjemahkan angka tersebut menjadi sebuah bilangan desimal:
Quest 7:
Di skema berikut ini pola bit 01101001 merepresentasikan angka berapa?
| Power of 2 | 0 | 1 | 1 | 0 | , | 1 | 0 | 0 | 1 |
|---|---|---|---|---|---|---|---|---|---|
| 8 | 4 | 2 | 1 | , | 0.5 | 0.25 | 0.125 | 0.0625 | |
Jawab: 4 + 2 + 0,5 + 0,0625 = 6,5625
Jumat, 26 April 2013
Basis Dua ke Basis Sepuluh
Ingat lagi bahwa X-n artinya 1/Xn. Maka 2-2 = 1/4 dan
Selama kamu mengitung, tetap jaga posisi dari bilang bulat dan posisi dari bilangan pecahan. Pada gambar di atas, baris atas adalah basis dua dan baris bawah adalah hasil konversinya ke basis sepuluh, sementara baris yang di tengah disebut polinomial.
2-3 = 1/8.
Untuk mengkonversi dari basis dua ke basis sepuluh, lakukan saja perhitungan seperti di atas. Berikut adalah 100,001 biner yang dikonvert ke desimal.
| 1 | 0 | 0 | , | 1 | 0 | 1 |
| 1×22 | 0×21 | 0×20 | , | 1×2-1 | 0×2-2 | 1×2-3 |
| 1×4 + | 0×2 + | 0×1+ | , | 1×0.5 + | 0×0.25 + | 1×0.125 |
| 4 + | 0 + | 0 + | , | 0.5 + | 0 + | 0.125 |
| 4 | , | 625 |
Quest 5: terjemahkan 0,112 menjadi basis 10
Jawab: 0,112 = 0×1 + 1×(0,5) + 1×(0,25) = 0,75
Notasi Posisi untuk Basis Dua
Notasi posisi juga bisa dipakai menggunakan selain basis sepuluh. Berikut adalah contoh menggunakan basis dua:
Saat sebuah basis tertentu tidak dicantumkan di dalam angka, maka digit ke 0 digunakan sebagai penanda pecahan. Tanda koma "," di tempat tersebut disebut binary point.
Secara umum, sebenarnya tanda koma tersebut digunakan untuk memisahkan pecahan dengan bilangan bulat yang disebut radix point. Di Amerika pemisahan tanda pecahan ini biasanya menggunakan tanda titik "."
| 1 | 0 | 0 | , | 1 | 0 | 1 |
| 1×22 | 0×21 | 0×20 | , | 1×2-1 | 0×2-2 | 1×2-3 |
Saat sebuah basis tertentu tidak dicantumkan di dalam angka, maka digit ke 0 digunakan sebagai penanda pecahan. Tanda koma "," di tempat tersebut disebut binary point.
Secara umum, sebenarnya tanda koma tersebut digunakan untuk memisahkan pecahan dengan bilangan bulat yang disebut radix point. Di Amerika pemisahan tanda pecahan ini biasanya menggunakan tanda titik "."
Quest 4: Cepat 1×2-1 ? Jawab menggunakan desimal
Jawab: 1×2-1 = 1/(21) = 1/2 = 0,5
Kamis, 25 April 2013
Notasi Posisi
Ini hanyalah notasi posisi dari angka desimal, yang tentu sudah kamu tahu sebelumnya. Koma desimal diletakkan di antara nilai kelipatan 100 dan 10-1.
Notasi 357,284 artinya 3 kali 100 + 5 kali 10 + 7 kali 1 + 2 kali 0,1 + 8 kali 0,01 + 4 kali 0,001.
Quest 3: Cepat 3/10 + 1/100 menggunakan notasi koma
Jawab: 0,31
| 3 | 5 | 7 | , | 2 | 8 | 4 |
| 3×102 | 5×101 | 7×100 | , | 2×10-1 | 8×10-2 | 4×10-3 |
Notasi 357,284 artinya 3 kali 100 + 5 kali 10 + 7 kali 1 + 2 kali 0,1 + 8 kali 0,01 + 4 kali 0,001.
Quest 3: Cepat 3/10 + 1/100 menggunakan notasi koma
Jawab: 0,31
BAB 29 — Pecahan dalam Biner
Sejauh ini kita telah melakukan perhitungan matematika dalam bentuk integer, baik yang two complement maupun yang unsigned integer. Bab ini akan mulai membahas tentang matematika floating point bisa dilakukan di MIPS.
Topik:
Topik:
- Notasi posisional dengan pecahan
- Konversi pecahan antara basis dua dengan basis sepuluh
- Representasi fixed point (koma tetap)
- Presisi yang terbatas dari pecahan biner (fixed point dan floating point)
- Bagaimana "seper sepuluh" tidak bisa diekspresikan menggunakan biner
- Program loop yang berbahaya
Quest 2: Di dalam angka desimal 12,6, berapakah faktor 10 dari tiap angka:
digit 1?
digit 2?
digit 6?
Jawab: digit 1 = 101
digit 2 = 100
digit 6 = 10-1
Rabu, 24 April 2013
Komplit fact()
Berikut adalah code fact() yang telah lengkap:
Quest 28: Adakah perbedaan konvensi linkage subroutine yang mengalir rekursif dengan yang tidak?
Jawab: Tidak ada, keduanya sama-sama berjalan dengan cara yang sama, yang spesial dari rekursif adalah dia memanggil dirinya sendiri.
# int fact( int n )
# {
# if ( n<=1)
# return 1;
# else
# return n*fact(n-1);
# }
.text
.globl fact
fact:
# prolog
sub $sp,$sp,4 # 1. Push return address
sw $ra,($sp)
sub $sp,$sp,4 # 2. Push caller's frame pointer
sw $fp,($sp)
sub $sp,$sp,4 # 3. Push register $s1
sw $s1,($sp)
sub $fp,$sp,0 # 4. $fp = $sp - space_for_variables (==0)
move $sp,$fp # 5. $sp = $fp
# body of subroutine
move $s1,$a0 # save argument in $s1
li $t1,1 # get a 1
bgt $s1,$t1,recurse # if ( n<=1)
li $v0,1 # return 1
b epilog
recurse: # else
# return n*fact(n-1)
sub $a0,$s1,1 # n-1
# subroutine call
# 1. No T registers to push
# 2. Argument is in $a0
jal fact # 3. Jump and link to subroutine
mul $v0,$v0,$s1 # n*fact(n-1)
epilog: # epilog
# 1. Return value is already in $v0
add $sp,$fp,0 # 2. $sp = $fp + space_for_variables (==0)
lw $s1,($sp) # 3. Pop register $s1
add $sp,$sp,4 #
lw $fp,($sp) # 4. Pop $fp
add $sp,$sp,4 #
lw $ra,($sp) # 5. Pop $ra
add $sp,$sp,4 #
jr $ra # 6. return to caller
Quest 28: Adakah perbedaan konvensi linkage subroutine yang mengalir rekursif dengan yang tidak?
Jawab: Tidak ada, keduanya sama-sama berjalan dengan cara yang sama, yang spesial dari rekursif adalah dia memanggil dirinya sendiri.
Memanggil Recursive
. . . . . .
recurse: # else
# return n*fact(n-1);
sub $a0,$s1,1 # argument0 = n-1
# subroutine call
# 1. No T registers to push
# 2. Argument is in $a0
jal fact # 3. Jump and link to subroutine
mul $v0,$v0,$s1 # n*fact(n-1)
epilog: # epilog
# 1. Return value is already in $v0
. . . . . .
jr $ra #
Rekursi telah diimplementasikan di sini menggunakan: (1) operasi mesin standar yang menggunakan eksekusi, testing dan percabangan. dan (2) runtime stack.
Ini adalah contoh abstraksi tingkat baru yang berada di atas tingkat dasar. Apakah menurut kamu ini adalah ide penting dalam ilmu komputer?
Quest 27: Bahasa pemrograman FORTRAN IV tidak mendukung rekursi. Apakah mungkin untuk membuat program rekursi menggunakan FORTRAN IV?
Jawab: Bisa, FORTRAN memiliki eksekusi yang berurutan, testing dan percabangan, seperti halnya semua bahasa. Untuk menulis sebuah program rekursif maka programmer harus mengalokasikan dan mengelola run-time stack, seperti dalam bahasa assembly. Bahasa modern tingkat tinggi melakukan hal ini secara otomatis.
Selanjutnya dari fact()
# int fact( int n )
# {
# if ( n<=1)
# return 1;
# else
# return n*fact(n-1);
# }
.text
.globl fact
fact:
# prolog
. . . . . .
# body of subroutine
move $s1,$a0 # save argument in $s1
li $t1,1 # get a 1
bgt $s1,$t1,recurse # if ( n<=1)
li $v0,1 # return 1
b epilog
recurse: # else
# return n*fact(n-1);
sub $a0,$s1,1 # argument0 = n-1
# subroutine call
# 1. No T registers to push
# 2. Argument is in $a0
jal fact # 3. Jump and link to subroutine
#
# value is returned in $v0
mul , , # n*fact(n-1)
epilog: # epilog
# 1. Return value is already in $v0
. . . . . .
jr $ra #
Percabangan dari if jika $s1 tidak sama dengan 1 atau kurang dari 1, adalah melompat ke symbolic address recurse yang melakukan pekerjaan n*fact(n-1). Dia pertama kali mengerjakan n-1 yang disimpan ke $a0 kemudian baru mengalikan.
Setelah itu dia memanggil fact(), tidak perlu kuatir untuk memanggil ulang karena setiap aktiuvasi akan menggunakan stacknya sendiri-sendiri.
Setelah memanggil fact(), register $v0 memegang return value (nilai hasil) dan register $s1 memegang nilai n.
Body dari fact()
Berikut adalah bagian dari isi subroutine fact().
Argumen yang berada di $a0 diamankan ke register $s1 karena kemungkinan nantinya register $a0 akan berubah. Secara subroutine ini menggunakan $s1 maka $s1 diamankan ke dalam stack saat prolog.
Operasi if di sini bekerja untuk mengecek apakah isi dari argumen $a0 yang sudah dipindah ke $s1 bernilai 1 atau kurang. Jika iya maka dia akan meletakkan nilai 1 ke register $v0 yang nantinya register ini akan digunakan sebagai accumulator. Jika tidak maka cabang lain akan diberlakukan.
# int fact( int n )
# {
# if ( n<=1)
# return 1;
# else
# return n*fact(n-1);
# }
.text
.globl fact
fact:
# prolog
. . . . . .
# body of subroutine
move $s1,$a0 # save argument in $s1
li $t1,1 # get a 1
bgt $s1,$t1,recurse # if ( n<=1)
li $v0,1 # return 1
b
recurse: # else
# return n*fact(n-1);
. . . . . .
epilog: # epilog
# 1. Return value is already in $v0
. . . . . .
jr $ra #
Argumen yang berada di $a0 diamankan ke register $s1 karena kemungkinan nantinya register $a0 akan berubah. Secara subroutine ini menggunakan $s1 maka $s1 diamankan ke dalam stack saat prolog.
Operasi if di sini bekerja untuk mengecek apakah isi dari argumen $a0 yang sudah dipindah ke $s1 bernilai 1 atau kurang. Jika iya maka dia akan meletakkan nilai 1 ke register $v0 yang nantinya register ini akan digunakan sebagai accumulator. Jika tidak maka cabang lain akan diberlakukan.
Senin, 22 April 2013
Entry Point (Titik Masuk)
Sekarang ke dalam subroutine. Alamat pertama dari subroutine ini disimbolkan dengn nama fact. Tentu saja nama fact hanyalah simbol yang dipakai oleh assembler, kenyataannya symbol ini akan diterjemahkan oleh assembler menjadi suatu letak atau alamat yang berada di main storage runtime. Alamat ini ditentukan oleh assembler, linker dan loader.
Simbol fact adalah simbol global (juga disebut simbol eksternal) sehingga assembler, linker dan loader bisa menggunakan simbol tersebut untuk menunjuk tempat yang sama di main memory.
Sebuah lokasi samacam fact ini yang mejadi target sebuah pemanggilan subroutine, disebut entry point. Kadang kala sebuah subroutine mempunyai beberap entri point, tiap-tiapnya berkaitan dengan fungsi yang berbeda-beda.
Quest 24: Apakah simbol global selalu meunjuk ke sebuah entry point?
Jawab: Tidak, bisa juga simbol global menunjuk ke suatu data yang diperlukan untuk operasi.
# int fact( int n )
# {
# if ( n<=1)
# return 1;
# else
# return n*fact(n-1);
# }
.text
.globl fact
fact:
# prolog
sub $sp,$sp,4 # 1. Push return address
sw $ra,($sp)
sub $sp,$sp,4 # 2. Push caller's frame pointer
sw $fp,($sp)
sub $sp,$sp,4 # 3. Push register $s1
sw $s1,($sp)
sub $fp,$sp,0 # 4. $fp = $sp - space_for_variables (==0)
move $sp,$fp # 5. $sp = $fp
# body of subroutine
. . . . . .
epilog: # epilog
# 1. Return value is already in $v0
add $sp,$fp,0 # 2. $sp = $fp + space_for_variables (==0)
lw $s1,($sp) # 3. Pop register $s1
add $sp,$sp,4 #
lw $fp,($sp) # 4. Pop $fp
add $sp,$sp,4 #
lw $ra,($sp) # 5. Pop $ra
add $sp,$sp,4 #
jr $ra # 6. return to caller
Simbol fact adalah simbol global (juga disebut simbol eksternal) sehingga assembler, linker dan loader bisa menggunakan simbol tersebut untuk menunjuk tempat yang sama di main memory.
Sebuah lokasi samacam fact ini yang mejadi target sebuah pemanggilan subroutine, disebut entry point. Kadang kala sebuah subroutine mempunyai beberap entri point, tiap-tiapnya berkaitan dengan fungsi yang berbeda-beda.
Quest 24: Apakah simbol global selalu meunjuk ke sebuah entry point?
Jawab: Tidak, bisa juga simbol global menunjuk ke suatu data yang diperlukan untuk operasi.
Komplit main()
Kembali ke contoh program yang kita buat.
Quest 23: Subroutine apa yang dipanggil oleh main()?
# main()
# {
# int a, b; // a: 0($fp), b: 4($fp)
# write("enter an int:")
# read( a );
# b = fact( a );
# write("factorial is:")
# print( b );
# }
.text
.globl main
main:
# prolog
sub $sp,$sp,4 # 1. Push return address
sw $ra,($sp)
sub $sp,$sp,4 # 2. Push caller's frame pointer
sw $fp,($sp)
# 3. No S registers to push
sub $fp,$sp,8 # 4. $fp = $sp - space_for_variables
move $sp,$fp # 5. $sp = $fp
# write("enter an int:")
li $v0,4 # print string service
la $a0,prompt1 # address of prompt
syscall
# read( a )
li $v0,5 # read integer service
syscall # $v0 gets the integer
sw $v0,0($fp) # save in variable a
# subroutine call
# 1. No T registers to push
lw $a0,0($fp) # 2. Put argument into $a0
jal fact # 3. Jump and link to subroutine
# return from subroutine
# 1. No T registers to restore
sw $v0,4($fp) # b = fact( a )
# write("factorial is:")
li $v0,4 # print string service
la $a0,prompt2 # address of prompt
syscall
# print( b )
lw $a0,4($fp) # load a into $a0
li $v0,1 # print integer service
syscall
# end the print line
li $v0,4 # print string service
la $a0,lf # address of line feed
syscall
# epilog
# 1. No return value
add $sp,$fp,8 # 2. $sp = $fp + space_for_variables
# 3. No S registers to pop
lw $fp,($sp) # 4. Pop $fp
add $sp,$sp,4 #
lw $ra,($sp) # 5. Pop $ra
add $sp,$sp,4 #
jr $ra # return to OS
.data
prompt1: .asciiz "enter an int:"
prompt2: .asciiz "factorial is:"
lf: .asciiz "\n"
Quest 23: Subroutine apa yang dipanggil oleh main()?
Kelas Storage
Ada 3 tempat di dalam memory yang bisa kita letakkan data: di data section (dideklarasikan dengan .data dalam bahasa assembly), di runtime-stack, dan di heap.
Subroutine boleh memiliki data yang tersimpan di section .data. Di bahasa pemrograman tingkat tinggi, seperti C, type penyimpanan ini disebut static.
Variabel yang disimpan dengan cara mengalokasikan run-time stack, biasanya disebut dengan variabel otomatis. Ini karena mereka secara otomatis di push dan di pop ketika subroutine masuk dan keluar. Biasanya kalau orang bilang "variabel" bisa mengacu ke "variabel otomatis".
Variabel yang tempat penyimpanannya ada di heap biasa disebut variabel dinamik. Bab 33 dari kuliah ini akan membahas tentang heap. Heap adalah tempat memory bagi object (menggunakan instruksi new kalau di Java atau C++). Di bahasa C memory dinamik dialokasikan menggunakan operasi malloc (atau sejenisnya).
Heap ada di atas data segment. Kalau variabel dinamik dialokasikan maka data segment akan tumbuh ke atas ke arah stack.
Quest 22: (mengulang) apa yang akan terjadi jika stack dan heap semakin membesar dan membesar?
Subroutine boleh memiliki data yang tersimpan di section .data. Di bahasa pemrograman tingkat tinggi, seperti C, type penyimpanan ini disebut static.
Variabel yang disimpan dengan cara mengalokasikan run-time stack, biasanya disebut dengan variabel otomatis. Ini karena mereka secara otomatis di push dan di pop ketika subroutine masuk dan keluar. Biasanya kalau orang bilang "variabel" bisa mengacu ke "variabel otomatis".
Variabel yang tempat penyimpanannya ada di heap biasa disebut variabel dinamik. Bab 33 dari kuliah ini akan membahas tentang heap. Heap adalah tempat memory bagi object (menggunakan instruksi new kalau di Java atau C++). Di bahasa C memory dinamik dialokasikan menggunakan operasi malloc (atau sejenisnya).
Heap ada di atas data segment. Kalau variabel dinamik dialokasikan maka data segment akan tumbuh ke atas ke arah stack.
Quest 22: (mengulang) apa yang akan terjadi jika stack dan heap semakin membesar dan membesar?
Sabtu, 20 April 2013
Selanjutnya dari main()
main() selanjutnya melakukan beberapa pekerjaan yaitu mencetak integer dan mencetak faktorialnya.
Akhirnya main() mengakhiri dengan epilog
Data yang ada di "prompt" tidak disimpan ke dalam stack.
Quest 21: Kenapa data variabel a dan b berbeda dengan data yang ada di prompt1 dan prompt2 ?
Jawab: a dan b adalah data yang hanya aktif saat subroutine dipanggil dan tidak aktif setelah kembali ke caller dengan begitu a dan b disimpan ke dalam stack
prompt1 dan prompt2 adalah data yang aktiv saat program berada di main memory, karenanya penyimpanannya ada di memory bagian penyimpanan data.
# print( b )
lw $a0,4($fp) # load b into $a0
li $v0,1 # print integer service
syscall
# end the print line
li $v0,4 # print string service
la $a0,lf # address of line feed
syscall
Akhirnya main() mengakhiri dengan epilog
# epilog # 1. No return value add $sp,$fp,8 # 2. $sp = $fp + space_for_variables # 3. No S registers to pop lw $fp,($sp) # 4. Pop $fp add $sp,$sp,4 # lw $ra,($sp) # 5. Pop $ra add $sp,$sp,4 # jr $ra # return to OS
Data yang ada di "prompt" tidak disimpan ke dalam stack.
.data
prompt1: .asciiz "enter an int:"
prompt2: .asciiz "factorial is:"
lf: .asciiz "\n"
Quest 21: Kenapa data variabel a dan b berbeda dengan data yang ada di prompt1 dan prompt2 ?
Jawab: a dan b adalah data yang hanya aktif saat subroutine dipanggil dan tidak aktif setelah kembali ke caller dengan begitu a dan b disimpan ke dalam stack
prompt1 dan prompt2 adalah data yang aktiv saat program berada di main memory, karenanya penyimpanannya ada di memory bagian penyimpanan data.
Isi dari main()
Bagian selanjutnya dari main(). Service SPIM untuk angka 4 dan 5 adalah untuk menampilkan string dan untuk membaca integer. Integer yang dimasukkan oleh user secara konvensi masuk ke dalam register $v0, kemudian disimpan sebagai variabel a yang ada di stack.
Kode selanjutnya mengerjakan b = fact(a). Hal ini dikerjakan dengan cara mengikuti protokol pemanggilan subroutine, dan menyimpan nilai hasil ke dalam b.
# write("enter an int:")
li $v0,4 # print string service
la $a0,prompt1 # address of prompt
syscall
# read( a )
li $v0,5 # read integer service
syscall # $v0 gets the integer
sw $v0,0($fp) # save in variable a
Kode selanjutnya mengerjakan b = fact(a). Hal ini dikerjakan dengan cara mengikuti protokol pemanggilan subroutine, dan menyimpan nilai hasil ke dalam b.
# subroutine call: b = fact( a )
# 1. No T registers to push
lw $a0,0($fp) # 2. Put argument into $a0
jal fact # 3. Jump and link to subroutine
# return from subroutine
# 1. No T registers to restore
sw $v0,4($fp) # b = fact( a )
Prolog main()
Berikut adalah main routine dari pseudo code dan prolog. Perhatikan bahwa di sini kita menggunakan 2 variabel.
# main()
# {
# int a, b; // a: 0($fp), b: 4($fp)
# write("enter an int:")
# read( a );
# b = fact( a );
# write("factorial is:")
# print( b );
# }
.text
.globl main
main:
# prolog
sub $sp,$sp,4 # 1. Push return address
sw $ra,($sp)
sub $sp,$sp,4 # 2. Push caller's frame pointer
sw $fp,($sp)
# 3. No S registers to push
sub $fp,$sp,8 # 4. $fp = $sp - space_for_variables
move $sp,$fp # 5. $sp = $fp
Rantai Aktifasi
Jika subroutine fact() dipanggil dengan argumen yang nilainya lebih besar dari 1 maka dia akan memanggil dirinya sendiri dengan argumen baru. Ini adalah aktifasi baru dengan code yang sama. Ini bukanlah masalah karena data untuk aktifasi pertama dari fact() telah di-push ke dalam stack. Aktifasi baru kini menggunakan stack baru dari frame stack data.
Jika aktifasi yang pertama mendapat kontrol kembali, maka dia akan menggunakan data yang sudah berada di tumpukan stack paling atas. Proses ini diilustrasikan seperti gambar di bawah. Tiap-tiap aktivasi direpresentasikan dengan lingkaran hjau. Tiap-tiap aktivasi ini bekerja dengan menggunakan datanya masing-masing yang berada di tumpukan frame stack. Tiap-tiap aktivasi ini tidak saling mengganggu satu sama lain.
# int fact( int n )
# {
# if ( n <= 1 )
# return 1;
# else
# return n*fact(n-1);
# }
Setiap lingkaran dari rantai aktivasi ini merepresentasikan aktivasi dari subroutine. Angka yang mendampingi panah ke bawah adalah argumen yang diberikan dan angka yang mendampingi panah ke atas adalah nilai yang dikembalikan.
Tiap-tiap satu lingkaran dalam rantai ini bersesuaian dengan satu frame stack yang ada di sampingnya. Saat pekerjaan ini selesai maka frame stack akan kembali memendek ke main dan rantai program pun juga memendek.
Jika aktifasi yang pertama mendapat kontrol kembali, maka dia akan menggunakan data yang sudah berada di tumpukan stack paling atas. Proses ini diilustrasikan seperti gambar di bawah. Tiap-tiap aktivasi direpresentasikan dengan lingkaran hjau. Tiap-tiap aktivasi ini bekerja dengan menggunakan datanya masing-masing yang berada di tumpukan frame stack. Tiap-tiap aktivasi ini tidak saling mengganggu satu sama lain.
# int fact( int n )
# {
# if ( n <= 1 )
# return 1;
# else
# return n*fact(n-1);
# }
Setiap lingkaran dari rantai aktivasi ini merepresentasikan aktivasi dari subroutine. Angka yang mendampingi panah ke bawah adalah argumen yang diberikan dan angka yang mendampingi panah ke atas adalah nilai yang dikembalikan.
Tiap-tiap satu lingkaran dalam rantai ini bersesuaian dengan satu frame stack yang ada di sampingnya. Saat pekerjaan ini selesai maka frame stack akan kembali memendek ke main dan rantai program pun juga memendek.
Contoh Program: Faktorial(N)
Contoh program kita selanjutnya adalah menyuruh user memasukkan interger, kemudian membaca integer tersebut dan mencetak faktorial dari interger tersebut. Berikut adalah gambaran output yang dihasilkan oleh program berikut pseudo-code nya.
Quest 17: Bagaimana cara menghitung faktorial?
Jawab: misal faktorial 5
fact(5) == 5*fact(4)
== 5*( 4*fact(3) )
== 5*( 4*( 3*fact(2)) )
== 5*( 4*( 3*(2*fact(1))) )
== 5*( 4*( 3*(2*1)) )
== 5*4*3*2*1
== 120
# main()
# {
# int a, b; // a: 0($fp), b: 4($fp)
# write("enter an int:")
# read( a );
# b = fact( a );
# write("factorial is:")
# print( b );
# }
# int fact( int n )
# {
# if ( n <= 1 )
# return 1;
# else
# return n*fact(n-1);
# }
Quest 17: Bagaimana cara menghitung faktorial?
Jawab: misal faktorial 5
fact(5) == 5*fact(4)
== 5*( 4*fact(3) )
== 5*( 4*( 3*fact(2)) )
== 5*( 4*( 3*(2*fact(1))) )
== 5*( 4*( 3*(2*1)) )
== 5*4*3*2*1
== 120
Kembali ke main()
Di contoh ini, main() tidak menyimpan register T manapun. Tidak ada yang perlu dilakukan saat dia mendapatkan kembali kontrol selain menggunakan nilai yang di letakkan ke $v0 sebagai hasil dari subroutine mysub().
Perhatikan kode di bawah, nilai yang tersimpan di $v0 dicopy ke variabel a yang berada di stack
Pada kalimat selanjutnya code akan bekerja menyalin nilai a di stack yang sudah memegang nilai $v0, ke dalam $a0 untuk kemudian dilakukan pencetakan nilai ini menggunakan service dari SPIM. Sekali lagi sebenarnya melakukan hal ini tidak perlu melibatkan stack, tetapi lagi-lagi kompiler yang tidak optimal mungkin melakukan hal semacam ini.
Kompiler yang optimal mungkin memproduksi code yang lebih efisien daripada code di atas.
Kompiler optimal mungkin akan memerikasa source kode dan menulis ulang source tersebut menjadi sebuah kalimat yang lebih efisien. Misalnya mengubah source code main() menjadi tanpa variabel a
main()
{
print( mysub( 6 ) );
}
# main()
# {
# int a; // a: 0($fp)
# a = mysub( 6 );
# print( a );
# }
.text
.globl main
main:
# prolog
sub $sp,$sp,4 # 1. Push return address
sw $ra,($sp)
sub $sp,$sp,4 # 2. Push caller's frame pointer
sw $fp,($sp)
# 3. No S registers to push
sub $fp,$sp,4 # 4. $fp = $sp - space_for_variables
move $sp,$fp # 5. $sp = $fp
# subroutine call
# 1. No T registers to push
li $a0,6 # 2. Put argument into $a0
jal mysub # 3. Jump and link to subroutine
# return from subroutine
# 1. No T registers to restore
sw $v0,0($fp) # a = mysub( 6 )
# print a
lw $a0,0($fp) # load a into $a0
li $v0,1 # print integer service
syscall
# epilog
# 1. No return value
add $sp,$fp,4 # 2. $sp = $fp + space_for_variables
# 3. No S registers to pop
lw $fp,($sp) # 4. Pop $fp
add $sp,$sp,4 #
lw $ra,($sp) # 5. Pop $ra
add $sp,$sp,4 #
jr $ra # return to OS
Perhatikan kode di bawah, nilai yang tersimpan di $v0 dicopy ke variabel a yang berada di stack
Pada kalimat selanjutnya code akan bekerja menyalin nilai a di stack yang sudah memegang nilai $v0, ke dalam $a0 untuk kemudian dilakukan pencetakan nilai ini menggunakan service dari SPIM. Sekali lagi sebenarnya melakukan hal ini tidak perlu melibatkan stack, tetapi lagi-lagi kompiler yang tidak optimal mungkin melakukan hal semacam ini.
Kompiler yang optimal mungkin memproduksi code yang lebih efisien daripada code di atas.
Kompiler optimal mungkin akan memerikasa source kode dan menulis ulang source tersebut menjadi sebuah kalimat yang lebih efisien. Misalnya mengubah source code main() menjadi tanpa variabel a
main()
{
print( mysub( 6 ) );
}
Subroutine Epilog
Epilog dari sebuah subroutine akan menyiapkan nilai yang akan dikembalikan ke caller. Dia kemudian mengembalikan register dan stack ke tempatnya milik caller agar nanti bisa dipakai lagi oleh caller. Akhirnya kontrol kembali ke caller.
Perhatikan bahwa code yang diperlukan untuk body sebuah subroutine di sini hanya sepanjang 5 kalimat, sementara total dari seluruh code menjadi 22 kalimat gara-gara konvensi linkage. Subroutine linkage membuatnya menjadi boros.
Quest 14: apa yang musti dilakukan oleh caller setelah mendapatkan kontrolnya kembali?
Jawab: dia musti merestore register T yang di awal-awal telah dia simpan sendiri
# int mysub( int arg )
# {
# int b,c; // b: 0($fp)
# // c: 4($fp)
# b = arg*2;
# c = b + 7;
#
# return c;
# }
.text
.globl mysub
mysub:
# prolog
sub $sp,$sp,4 # 1. Push return address
sw $ra,($sp)
sub $sp,$sp,4 # 2. Push caller's frame pointer
sw $fp,($sp)
sub $sp,$sp,4 # 3. Push register $s1
sw $s1,($sp)
sub $fp,$sp,8 # 4. $fp = $sp - space_for_variables
move $sp,$fp # 5. $sp = $fp
# body of subroutine
mul $s1,$a0,2 # arg*2
sw $s1,0($fp) # b = " "
lw $t0,0($fp) # get b
add $t0,$t0,7 # b+7
sw $t0,4($fp) # c = " "
# epilog
lw $v0,4($fp) # 1. Put return value in $v0
add $sp,$fp,8 # 2. $sp = $fp + space_for_variables
lw $s1,($sp) # 3. Pop register $s1
add $sp,$sp,4 #
lw $fp,($sp) # 4. Pop $fp
add $sp,$sp,4 #
lw $ra,($sp) # 5. Pop $ra
add $sp,$sp,4 #
jr $ra # 6. return to caller
Perhatikan bahwa code yang diperlukan untuk body sebuah subroutine di sini hanya sepanjang 5 kalimat, sementara total dari seluruh code menjadi 22 kalimat gara-gara konvensi linkage. Subroutine linkage membuatnya menjadi boros.
Quest 14: apa yang musti dilakukan oleh caller setelah mendapatkan kontrolnya kembali?
Jawab: dia musti merestore register T yang di awal-awal telah dia simpan sendiri
Menggunakan Variabel
Subroutine ini menggunakan dua variabel, jadi dialokasikan ruang sepanjang 8byte untuk mereka.
Program ini menjadi tidak efisien. Sebenarnya tidak perlu menyetore b kemudian meloadnya. Sebuah kompiler yang tidak optimal melakukan hal seperti ini, bagaimanapun juga.
Quest 12: Fill in the blank. Anggap bahwa variabel b terletak sejauh 0 dari $fp dan variabel c terletak sejauh 4 dari $fp
# int mysub( int arg )
# {
# int b,c; // b: 0($fp)
# // c: 4($fp)
# b = arg*2;
# c = b + 7;
#
# return c;
# }
.text
.globl mysub
mysub:
# prolog
sub $sp,$sp,4 # 1. Push return address
sw $ra,($sp)
sub $sp,$sp,4 # 2. Push caller's frame pointer
sw $fp,($sp)
sub $sp,$sp,4 # 3. Push register $s1
sw $s1,($sp)
sub $fp,$sp,8 # 4. $fp = $sp - space_for_variables
move $sp,$fp # 5. $sp = $fp
# body of subroutine
mul $s1,$a0,2 # arg*2
sw $s1, ( ) # b = " "
lw $t0, ( ) # get b
add $t0,$t0, # b+7
sw $t0, ( ) # c = " "
. . . . .
jr $ra # return to caller
Program ini menjadi tidak efisien. Sebenarnya tidak perlu menyetore b kemudian meloadnya. Sebuah kompiler yang tidak optimal melakukan hal seperti ini, bagaimanapun juga.
Quest 12: Fill in the blank. Anggap bahwa variabel b terletak sejauh 0 dari $fp dan variabel c terletak sejauh 4 dari $fp
Prolog untuk mysub()
Tentu saja mysub() harus diawali dengan prolog. Ada dua variabel, jadi alokasi akan dilakukan ke dalam stack.
Subroutine ini seharusnya ditulis tanpa melibatkan $s1. Perhatikan code di atas
# int mysub( int arg )
# {
# int b,c; // b: 0($fp)
# // c: 4($fp)
# b = arg*2;
# c = b + 7;
#
# return c;
# }
.text
.globl
:
# prolog
sub $sp,$sp,4 # 1. Push return address
sw $ra,($sp)
sub $sp,$sp,4 # 2. Push caller's frame pointer
sw $fp,($sp)
, , # 3. Push register $s1
,
sub $fp,$sp, # 4. $fp = $sp - space_for_variables
move $sp,$fp # 5. $sp = $fp
. . . .
jr $ra # return to caller
Subroutine ini seharusnya ditulis tanpa melibatkan $s1. Perhatikan code di atas
Memanggil Subroutine
Pada titik ini kita telah "mengkompilasi" tiga baris pertama dari program bahasa "C" ke dalam bahasa assembly. Selanjutnya program akan memanggil subroutine mysub(), silahkan lihat kode selanjutnya di bawah ini:
# main() # { # int a; # a = mysub( 6 ); # print( a ); # } .text .globl main main: # prolog sub $sp,$sp,4 # 1. Push return address sw $ra,($sp) sub $sp,$sp,4 # 2. Push caller's frame pointer sw $fp,($sp) # 3. No S registers to push addiu $fp,$sp,4 # 4. $fp = $sp + space_for_variables move $sp,$fp # 5. $sp = $fp # subroutine call # 1. No T registers to push li $a0,6 # 2. Put argument into $a0 jal mysub # 3. Jump and link to subroutine # return from subroutine . . . . # epilog jr $ra # return to OS
main()
Di bawah ini adalah code untuk main(), dengan beberapa kotak kosong. Aturan untuk prolog subroutine disalin dari atas.
Quest 9: Fill in the blank seperti yang dimaksud oleh koment
# main()
# {
# int a;
# a = mysub( 6 );
# print( a );
# }
.text
.globl main
main:
# prolog
sub $sp,$sp,4 # 1. Push return address
sw $ra,($sp)
sub $sp,$sp,4 # 2. Push caller's frame pointer
sw $fp,($sp)
# 3. No S registers to push
sub , , # 4. $fp = $sp - space_for_variables
$sp,$fp # 5. $sp = $fp
# subroutine call
. . . .
# return from subroutine
. . . .
# epilog
jr $ra # return to OS
Quest 9: Fill in the blank seperti yang dimaksud oleh koment
Contoh Program
Jumlah register yang dimiliki MIPS (atau processor yang lain) tidak membatasi banyaknya variabel yang dimiliki oleh subroutine. Sebanyak variabel yang kamu inginkan selama bisa dialokasikan ke dalam stack. Berikut adalah contoh program yang ditulis dalam bahasa C:
Bagi operating system, main() adalah subroutine. Jika main() mendapat kontrol maka dia harus mengikuti aturan di bawah "subroutine prolog".
Quest 8: berapa banyak ruangan yang musti diberikan stack untuk menyimpan variabel-variabel yang ada di main() ?
Jawab: 4byte untuk sebuah variabel a
main() { int a; a = mysub( 6 ); print( a ); } int mysub( int arg ) { int b,c; b = arg*2; c = b + 7; return c; }
Bagi operating system, main() adalah subroutine. Jika main() mendapat kontrol maka dia harus mengikuti aturan di bawah "subroutine prolog".
Quest 8: berapa banyak ruangan yang musti diberikan stack untuk menyimpan variabel-variabel yang ada di main() ?
Jawab: 4byte untuk sebuah variabel a
Kamis, 18 April 2013
Diagram
Aturan ini adalah rumit. Secara garis besar cara kerjanya sama dengan bab sebelumnya tentang konvensi linkage berbasis stack. Tapi sekarang, prolog subroutine menumpuk sejumlah ruangan di dalam stack untuk digunakan sebagai variabel lokal, dan di epilog mereka menge pop out.
Inilah gambarannya. Gambar menunjukkan bagian dari subroutine linkage, tugas-tugas dasarnya adalah sebagai berikut:
Memanggil subroutine: Tumpuk register T yang memegang nilai yang perlu diamankan. Letakkan argumen di register A. jal ke subroutine
Prolog: Tumpuk $ra dan $fp milik caller, tumpuk register S. Inisialisasi $fp dan $sp milik diri sendiri
Body: Normal code, kecuali jika dia memanggil subroutine lainnya maka aturan akan berlaku. Register T dan register A boleh digunakan secara bebas sebagaimana S yang telah diamankan sebelumnya. Akses ke variabel lokal menggunakan distance($fp).
Epilog: Letakkan nilai hasil ke dalam register V. Reset $sp melewati ruangan variable. Pop register S, pop $fp milik caller dan $ra. Kembali ke caller dengan jr $ra
Mendapatkan kontrol kembali: Pop out register T yang telah diamankan
Inilah gambarannya. Gambar menunjukkan bagian dari subroutine linkage, tugas-tugas dasarnya adalah sebagai berikut:
Memanggil subroutine: Tumpuk register T yang memegang nilai yang perlu diamankan. Letakkan argumen di register A. jal ke subroutine
Prolog: Tumpuk $ra dan $fp milik caller, tumpuk register S. Inisialisasi $fp dan $sp milik diri sendiri
Body: Normal code, kecuali jika dia memanggil subroutine lainnya maka aturan akan berlaku. Register T dan register A boleh digunakan secara bebas sebagaimana S yang telah diamankan sebelumnya. Akses ke variabel lokal menggunakan distance($fp).
Epilog: Letakkan nilai hasil ke dalam register V. Reset $sp melewati ruangan variable. Pop register S, pop $fp milik caller dan $ra. Kembali ke caller dengan jr $ra
Mendapatkan kontrol kembali: Pop out register T yang telah diamankan
Langganan:
Komentar (Atom)






